JZ70 矩形覆盖

发表于 分类于 本文字数： 459 阅读时长 ≈ 2 分钟

JZ70 矩形覆盖

描述

我们可以用 21 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 21 的小矩形无重叠地覆盖一个 2*n 的大矩形，从同一个方向看总共有多少种不同的方法？

数据范围：$0≤n≤38$
进阶：空间复杂度 $O(1)$ ，时间复杂度 $O(n)$

注意：约定 $n == 0$ 时，输出 0

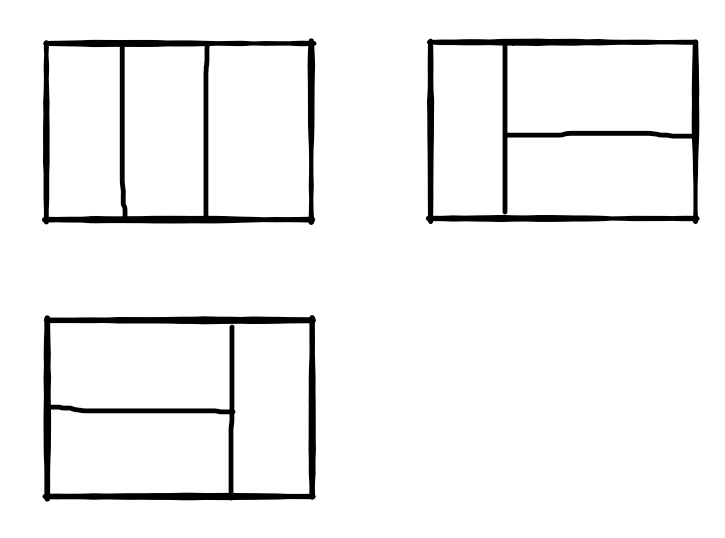
比如$n=3$时，2*3的矩形块有3种不同的覆盖方法(从同一个方向看)：

img

输入描述：2*1的小矩形的总个数n

返回值描述：覆盖一个2*n的大矩形总共有多少种不同的方法(从同一个方向看)

示例1

1
2
输入：0
返回值：0

示例2

1
2
输入：1
返回值：1

示例3

1
2
输入：4
返回值：5

题解

同样的拆解子问题，我们考虑$dp[i]$和$dp[i-1]$或者更早的$dp$之间的关系，当已经放置$i-1$块以后，我们直接在它的右侧再竖着放置一块可以得到一种解决方案，这种方案有$dp[i-1]$种。如果考虑在已经放置了$i-2$块以后再放两块，放置两块的方法共有两种，那么这种情况就有$dp[i-2]*2$种方案，但是其中有一种会和前面的$i-1$块时的重复，那么实际上只有$dp[i-2]$种独特方案。继续再往前思考，若是已经放置了$i-3$块，则这种情况下无论怎么放置都会和前面已经分析过的重复，所以$dp[i] = dp[i-1]+dp[i-2]$，初始条件$dp[1]=1,dp[2]=2$

代码

1
2
3
4
5
6
7
class Solution {
public:
    int rectCover(int number) {
        if(number==0||number==1||number==2) return number;
        return rectCover(number-1)+rectCover(number-2);
    }
};