JZ86 在二叉树中找到两个节点的最近公共祖先

发表于 分类于 本文字数： 458 阅读时长 ≈ 2 分钟

JZ86 在二叉树中找到两个节点的最近公共祖先

描述

给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2，请找到 o1 和 o2 的最近公共祖先节点。

数据范围：树上节点数满足$1≤n≤105$, 节点值val满足区间 [0,n)

要求：时间复杂度$O(n)$

注：本题保证二叉树中每个节点的$val$值均不相同。

1
如当输入{3,5,1,6,2,0,8,#,#,7,4},5,1时，二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示：

img

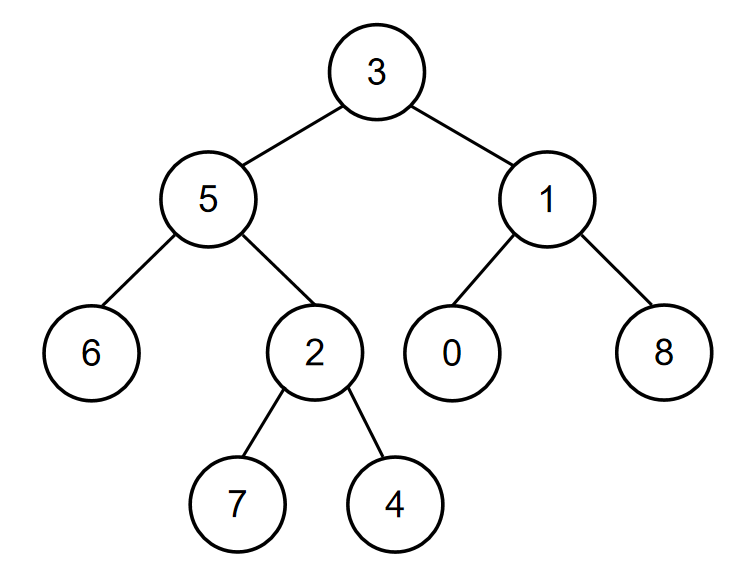
所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3，所以对应的输出为3。

节点本身可以视为自己的祖先

示例1

1
2
输入：{3,5,1,6,2,0,8,#,#,7,4},5,1
返回值：3

示例2

1
2
输入：{3,5,1,6,2,0,8,#,#,7,4},2,7
返回值：2

题解

初见思路：从23号回家开始就一直没写，这道题倒是很早就看了，刚看的时候也没有思路，后面想明白了，用前面写过的找某节点的路径，这道题中确定了给出的o1和o2一定在树中，所以只要分别找到它们到根节点的路径，然后进行对比就可以找到它们的最近公共祖先了(从上到下的最后一个公共祖先)。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
#include <vector>
using namespace std;

class Solution {
public:
    int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
        vector<int> path1, path2;
        findPath(root, o1, path1);
        findPath(root, o2, path2);

        int i = 0;
        while (i < path1.size() && i < path2.size() && path1[i] == path2[i]) {
            i++;
        }
        return path1[i - 1]; // 最近公共祖先
    }

private:
    bool findPath(TreeNode* root, int target, vector<int>& path) {
        if (!root) return false;
        path.push_back(root->val);

        if (root->val == target) return true;
        if (findPath(root->left, target, path) || findPath(root->right, target, path)) {
            return true;
        }

        path.pop_back(); // 回溯
        return false;
    }
};