JZ68 二叉搜索树的最近公共祖先

发表于 分类于 本文字数： 566 阅读时长 ≈ 2 分钟

JZ68 二叉搜索树的最近公共祖先

描述

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

1.对于该题的最近的公共祖先定义:对于有根树T的两个节点p、q，最近公共祖先LCA(T,p,q)表示一个节点x，满足x是p和q的祖先且x的深度尽可能大。在这里，一个节点也可以是它自己的祖先.

2.二叉搜索树是若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值； 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值

3.所有节点的值都是唯一的。

4.p、q 为不同节点且均存在于给定的二叉搜索树中。

数据范围:

$3<=节点总数<=10000$

$0<=节点值<=10000$

如果给定以下搜索二叉树: {7,1,12,0,4,11,14,#,#,3,5}，如下图:

img

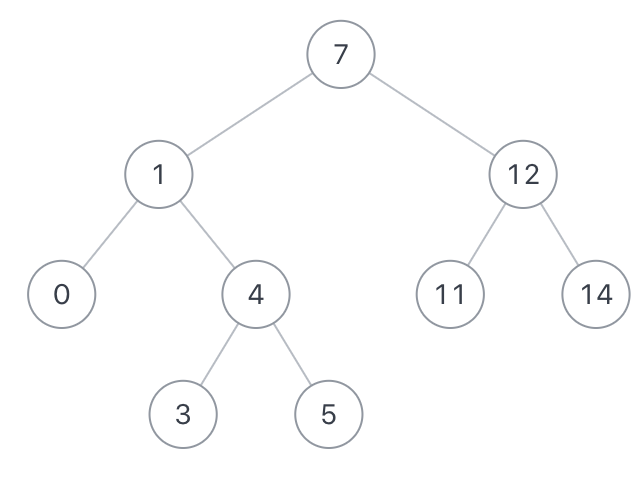
示例1

1
2
3
输入：{7,1,12,0,4,11,14,#,#,3,5},1,12
返回值：7
说明：节点1 和 节点12的最近公共祖先是7

示例1

1
2
3
输入：{7,1,12,0,4,11,14,#,#,3,5},12,11
返回值：12
说明：因为一个节点也可以是它自己的祖先.所以输出12

题解

初见思路：这道题其实可以用和 JZ86一样的方法来做，但是如果这样的话就没有用到二叉搜索树的性质，试一试利用二叉搜索树的性质来优化一下做吧。

二叉搜索树的特性是，一个根节点的左侧一定比它小，而右侧一定比它大。由此我们可以判断每个节点在二叉搜索树的哪一侧，当出现分叉时则找到了最近的公共根节点。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * struct TreeNode {
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 *	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param root TreeNode类 
     * @param p int整型 
     * @param q int整型 
     * @return int整型
     */
    int lowestCommonAncestor(TreeNode* root, int p, int q) {
        while(root){
            if(p<root->val && q<root->val){
                root = root->left;
            }else if (p>root->val && q >root->val){
                root = root->right;
            }else{
                return root->val;
            }
        }
        
        return -1;
    }
};