按之字形顺序打印二叉树

发表于 更新于 分类于 本文字数： 707 阅读时长 ≈ 3 分钟

JZ77 按之字形顺序打印二叉树

描述

给定一个二叉树，返回该二叉树的之字形层序遍历，（第一层从左向右，下一层从右向左，一直这样交替）

数据范围：0≤n≤15000≤n≤1500,树上每个节点的val满足 ∣val∣<=1500∣val∣<=1500
要求：空间复杂度：O(n)O(n)，时间复杂度：O(n)O(n)

例如：

1
给定的二叉树是{1,2,3,#,#,4,5}

imgs

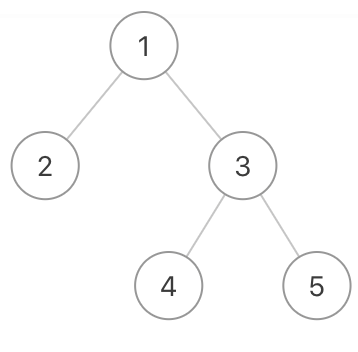
该二叉树之字形层序遍历的结果是
[
[1],
[3,2],
[4,5]
]

示例1

1
2
3
输入：{1,2,3,#,#,4,5}
返回值：[[1],[3,2],[4,5]]
说明：如题面解释，第一层是根节点，从左到右打印结果，第二层从右到左，第三层从左到右。

示例2

1
2
输入：{8,6,10,5,7,9,11}
返回值：[[8],[10,6],[5,7,9,11]]

示例3

1
2
输入：{1,2,3,4,5}
返回值：[[1],[3,2],[4,5]]

题解

初见思路：首先是要理解这个之字形，然后注意到题中是把各层存储到数组中进行返回，那么我们可以首先根据层数把它们统一放置在各层的数组中，然后再根据层数来决定是否反转这一层的排序。

进一步思考可以想到，如果放在数组里面再反转比先反转再放进数组要麻烦，所以只要先把需要反转的层的左右子树的数值交换即可。(偶数层交换)

最后确定顺序，如果先交换的话，那么只需要进行层序遍历($BFS$)即可，使用队列实现。

改进：思路很正确，但是实践中出现了一些问题，反转子树确实是个灵光一现的方法，但是它会让后续的子树也反转，所以还是在存储的时候反向存进数组即可。另外使用队列的时候，每一次$while$循环期间，队列里面的元素都是同一层的，只需要追踪这一层的层深，然后在循环开始时统计队列中的元素数量(便于反向存入数组)，在每一次循环结束前给层深+1即可。代码中是使用每层变化$Flag$的方式来实现的追踪层深。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * struct TreeNode {
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 *	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param pRoot TreeNode类 
     * @return int整型vector<vector<>>
     */
    vector<vector<int>> Print(TreeNode* pRoot) {
        vector<vector<int>> res;
        if (!pRoot) return res;

        queue<TreeNode*> q;
        q.push(pRoot);
        bool leftToRight = true;  // 标记打印方向

        while (!q.empty()) {
            int size = q.size();
            vector<int> level(size);
            for (int i = 0; i < size; i++) {
                TreeNode* node = q.front();
                q.pop();

                // 根据方向决定存放位置
                int index = leftToRight ? i : size - 1 - i;
                level[index] = node->val;

                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
            res.push_back(level);
            leftToRight = !leftToRight; // 交替方向
        }

        return res;
    }
};