二叉搜索树与双向链表

发表于 更新于 分类于 本文字数： 776 阅读时长 ≈ 3 分钟

JZ36 二叉搜索树与双向链表

描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。如下图所示

imgs

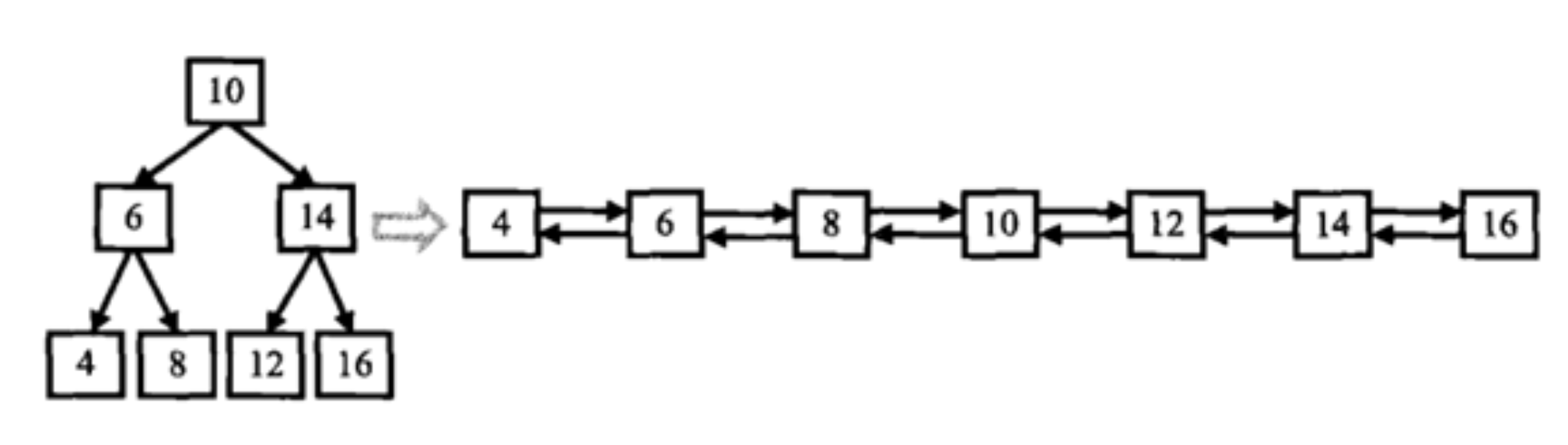
数据范围：输入二叉树的节点数 $0≤n≤1000$，二叉树中每个节点的值 $0≤val≤1000$
要求：空间复杂度$O(1)$（即在原树上操作），时间复杂度 $O(n)$

注意:

  • 要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继
  • 返回链表中的第一个节点的指针
  • 函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构
  • 你不用输出双向链表，程序会根据你的返回值自动打印输出

**输入描述：**二叉树的根节点

返回值描述：双向链表的其中一个头节点。

示例1

1
2
3
4
5
输入：{10,6,14,4,8,12,16}
返回值：
From left to right are:4,6,8,10,12,14,16;
From right to left are:16,14,12,10,8,6,4;
说明：输入题面图中二叉树，输出的时候将双向链表的头节点返回即可。

示例2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
输入：{5,4,#,3,#,2,#,1}
返回值：
From left to right are:1,2,3,4,5;
From right to left are:5,4,3,2,1;
说明：
                    5
                  /
                4
              /
            3
          /
        2
      /
    1
树的形状如上图

题解

初见思路：题面很复杂，但是实际上就是首先对二叉搜索树进行左中右的中序遍历，然后在遍历的过程中根据顺序把链表建立起来即可。难度大概是在实现上面，要实现中序遍历也就是DFS的话应该用堆会好一些。

好难，完全没有思路，前面的思路也没有什么好的实现方法。

问了大G老师，我在实现的时候试着去保存$pre$变量，也考虑到了每次访问栈顶的时候一定是访问到了栈中的最小元素，但是没有高明白怎么在不影响后续堆栈的同时去修改指针指向，整了一堆(比如说再$pop$出来一个等等)，看了大G老师的才明白大道至简，让$pre$的$right$指向$curr$，再把$curr$的$left$指向$pre$就行了，反正后续堆栈只用的到$curr\rightarrow right$。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
#include <stack>
class Solution {
  public:
    TreeNode* Convert(TreeNode* pRootOfTree) {
        if (!pRootOfTree) return nullptr;

        stack<TreeNode*> st;
        TreeNode* curr = pRootOfTree;
        TreeNode* pre = nullptr;
        TreeNode* head = nullptr;

        while (curr != nullptr || !st.empty()) {
            // 将当前节点及其所有左子节点压入栈中
            while (curr != nullptr) {
                st.push(curr);
                curr = curr->left;
            }

            // 当前节点为空，栈顶元素就是左子树的最深节点
            curr = st.top();
            st.pop();

            // 处理当前节点
            if (pre == nullptr) {
                head = curr;  // 保存链表的头
            } else {
                pre->right = curr;  // 前一个节点的右指针指向当前节点
                curr->left = pre;   // 当前节点的左指针指向前一个节点
            }

            pre = curr;  // 更新前一个节点为当前节点

            // 处理当前节点的右子树
            curr = curr->right;
        }

        return head;
    }
};