拼劲全力做出来了一个时间复杂度$O(n)$的方法,最后还是TLE,然后查了一下才知道,$set$本身会吃很多复杂度,在最差情况下会额外增加$O(n)$的复杂度,所以$set$还是慎用的好。
题目描述
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。
图用一个大小为 n 下标从 0 开始的数组 edges 表示,节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边,那么 edges[i] == -1 。
请你返回图中的 最长 环,如果没有任何环,请返回 -1 。
一个环指的是起点和终点是 同一个 节点的路径。
示例
示例1:
1
2
3
4
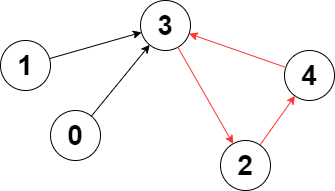
| 输入:edges = [3,3,4,2,3]
输出去:3
解释:图中的最长环是:2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ,所以返回 3 。
|
示例2:
1
2
3
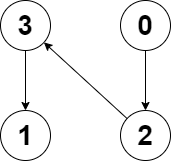
| 输入:edges = [2,-1,3,1]
输出:-1
解释:图中没有任何环。
|
提示:
1
2
3
4
| n == edges.length
2 <= n <= 105
-1 <= edges[i] < n
edges[i] != i
|
题解:遍历
每个节点至多只有一个出边,所以说一个节点我们不管在什么情况下都只需要访问一次,访问一次过后这个节点不管是不是环的一部分,我们都不需要再一次访问它。然后我们只需要记录下每个节点在访问时是在路径上的第几个位置访问的即可,因为当访问到环尾时,只需要将环尾的访问路径位置减去环首的访问路径位置即可获得该环的长度。
我的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
public:
int longestCycle(vector<int>& edges) {
int n = edges.size();
int ans = -1;
set<int> indexs;
for(int i = 0; i < n; i++){
indexs.insert(i);
}
while(!indexs.empty()){
int next = *indexs.begin();
map<int,int> path;
int path_index = 0;
while(next!=-1){
indexs.erase(next);
path[next] = path_index;
path_index +=1;
next = edges[next];
if(next!=-1 && (path.find(next)!=path.end() || path.count(next)!=0)){
break;
}
}
if(next!=-1){
if(path_index - path[next] > ans)
ans = path_index - path[next];
}
}
return ans;
}
};
|
复杂度分析:
题解代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
int longestCycle(vector<int>& edges) {
int n = edges.size();
vector<int> label(n);
int current_label = 0, ans = -1;
for (int i = 0; i < n; ++i) {
if (label[i]) {
continue;
}
int pos = i, start_label = current_label;
while (pos != -1) {
++current_label;
if (label[pos]) {
if (label[pos] > start_label) {
ans = max(ans, current_label - label[pos]);
}
break;
}
label[pos] = current_label;
pos = edges[pos];
}
}
return ans;
}
};
|
复杂度分析:


