LeetCode2614

发表于 更新于 分类于 ， 本文字数： 575 阅读时长 ≈ 2 分钟

LeetCode.2614:对角线上的质数

​ 今天做的2711和对角线相关，所以今天就把之前做的一道同是对角线相关的题目抬上来(才不是因为简单难度好写)。

题目描述

给你一个下标从 0 开始的二维整数数组 nums 。

返回位于 nums 至少一条 对角线 上的最大 质数 。如果任一对角线上均不存在质数，返回 0 。

注意：

  • 如果某个整数大于 1 ，且不存在除 1 和自身之外的正整数因子，则认为该整数是一个质数。
  • 如果存在整数 i ，使得 nums[i][i] = val 或者 nums[i][nums.length - i - 1]= val ，则认为整数 val 位于 nums 的一条对角线上。

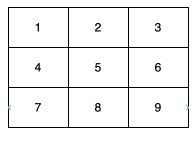
在上图中，一条对角线是 [1,5,9] ，而另一条对角线是 [3,5,7] 。

示例

示例1：

1
2
3
输入：nums = [[1,2,3],[5,6,7],[9,10,11]]
输出：11
解释：数字 1、3、6、9 和 11 是所有 "位于至少一条对角线上" 的数字。由于 11 是最大的质数，故返回 11 。

示例2：

1
2
3
输入：nums = [[1,2,3],[5,17,7],[9,11,10]]
输出：17
解释：数字 1、3、9、10 和 17 是所有满足"位于至少一条对角线上"的数字。由于 17 是最大的质数，故返回 17 。

提示：

1
2
3
1 <= nums.length <= 300
nums.length == numsi.length
1 <= nums[i][j] <= 4*106

题解

​ 这道题的题解重点在于两点，第一点是对角线的判断，第二点是质数的判断。对角线很简单，遍历时i=j即为主对角线元素，i=i,j=n-i-1为副对角线元素，但这道题只需要对角线，那么就可以直接去找nums[i][i]和nums[i][n-i-1]即为每一行的对角线元素。质数的判断在初学C语言的时候基本都学过，把这个数从2开始，一直除到这个数字的开方为止，即为最快的求质数方法。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public boolean check(int val){
        if(val <= 1){
            return false;
        }
        int check = 2;
        while(check <= Math.sqrt(val)){
            if(val % check == 0){
                return false;
            }
            check+=1;
        }
        return true;
    }
    public int diagonalPrime(int[][] nums) {
        int n = nums[0].length;
        int left = 0;
        int right = 0;
        int ans = 0;
        for(int i = 0; i < n; i++){
            if(ans < nums[i][i] && check(nums[i][i])){
                ans = nums[i][i];
            }

            if(ans < nums[i][n - i - 1] && check(nums[i][n - i - 1])){
                ans = nums[i][n - i - 1];
            }
        }

        return ans;
    }
}